期刊名：Mathematics

期刊主页：https://www.mdpi.com/journal/mathematics

“函数插值”是 Mathematics 期刊“应用数学”栏目的子栏目之一，致力于推广函数插值这一新兴数学框架的理论发展及其在多学科领域中的创新应用。本栏目重点关注函数插值在微分方程、变分法、优化算法、延拓方法、反问题求解、刚性系统与混合系统等方向中的创新应用，尤其欢迎能够通过嵌入约束显著提升现有数值方法精度、效率或稳定性的研究文章。同时，也鼓励作者就函数插值与拉格朗日乘数法等传统方法进行对比分析，或将其与现有计算架构结合以解决工程、物理与科学计算问题。

目前，该栏目由栏目主编Daniele Mortari教授主持，编委会由8位来自全球的知名学者组成，其中包括北京师范大学袁文教授、美国麻省理工学院Richard Linares教授、意大利卡拉布里亚大学Francesco Aldo Costabile教授、西班牙萨拉戈萨大学Antonio Elipe教授等多位权威专家。

本期将为您精选该栏目3篇优质文章，希望能为相关领域学者提供更多灵感启发，欢迎各位阅读。

栏目主编：Prof. Dr. Daniele Mortari，德克萨斯农工大学

现任德克萨斯农工大学航空航天工程教授，德克萨斯农工大学ASTRO中心空间首席科学家。从事姿态和位置估计、卫星星座设计、传感器数据处理以及线性代数和数值算法方面的各种课题研究。其工作得到了广泛认可，包括获得美国科学院/国际宇航科学院颁发的最佳论文奖、3项美国国家航空航天局团体成就奖、2007年电气电子工程师学会Judith A. Resnik奖以及2016年美国科学院Dirk Brouwer奖。发表了约120篇期刊论文、240篇会议论文，并应邀举办了100场研讨会。国际宇航科学院院士、IEEE和AAS Fellow、AIAA Associate Fellow、IEEE-AESS空间系统技术小组荣誉成员和前IEEE杰出演讲人。

文章推荐：

1. Theory of Functional Connections Extended to Fractional Operators

函数连接理论扩展到分数阶算子

Daniele Mortari, Roberto Garrappa and Luigi Nicolò

https://www.mdpi.com/2231128

文章亮点

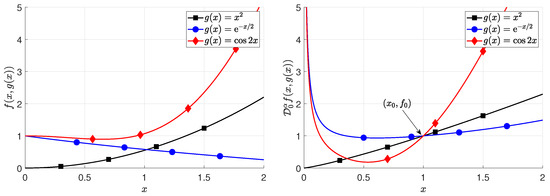
(1) 本文首次将函数连接理论 (Theory of Functional Connections, TFC) 扩展到分数阶算子 (包括分数阶导数和积分)，为处理分数阶约束问题提供了一个全新的、通用的解析框架。

(2) 基于扩展后的TFC理论，搭建了分数阶约束问题的系统的求解框架，能推导出代表所有受分数阶约束条件限制的函数的表达式。

(3) 该扩展已通过三个数值示例 (单约束、混合约束、线性组合约束) 得到验证。

扫描二维码，阅读英文原文：

原文出自 Mathematics

Mortari, D.; Garrappa, R.; Nicolò, L. Theory of Functional Connections Extended to Fractional Operators. Mathematics 2023, 11, 1721.

2. Physics-Informed Neural Networks and Functional Interpolation for Solving the Matrix Differential Riccati Equation

求解矩阵微分Riccati方程的物理信息神经网络与函数插值

Kristofer Drozd et al.

https://www.mdpi.com/244597

文章亮点

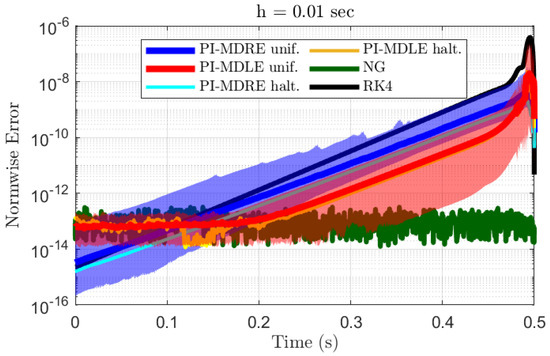
(1) 本研究首次将极限函数连接理论 (X-TFC) 应用于求解矩阵微分Riccati方程 (MDRE) 这一重要的控制领域问题。

(2) 提出并比较了直接法和间接法两种求解路径。

(3) 论文还通过与其他主流方法在精度、计算时间、泛化能力等方面的详细对比，明确了两种X-TFC策略的优缺点和适用场景，并指出了未来改进方向。

扫描二维码，阅读英文原文

原文出自 Mathematics

Drozd, K.; Furfaro, R.; Schiassi, E.; D’Ambrosio, A. Physics-Informed Neural Networks and Functional Interpolation for Solving the Matrix Differential Riccati Equation. Mathematics 2023, 11, 3635.

3. Lipschitz Transformations and Maurey-Type Non-Homogeneous Integral Inequalities for Operators on Banach Function Spaces

Banach函数空间上算子的Lipschitz变换与Maurey型非齐次积分不等式

Roger Arnau and Enrique A. Sánchez-Pérez

https://www.mdpi.com/2554678

文章亮点

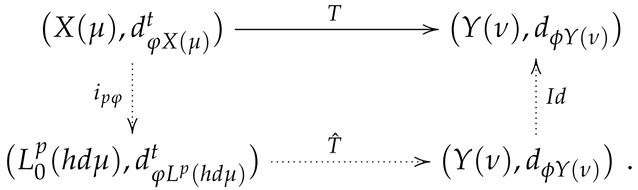
(1) 本文提出了一种基于Lipschitz点值变换的方法，用于在Banach函数空间中根据其范数定义距离。

(2) 引入了非齐次表达式，将向量范数不等式转化为涉及非齐次表达式的算子的积分支配关系，这是与经典的Maurey型分析方法的主要区别。

(3) 证明了函数值域受限于特定区间时算子的积分不等式，并以洛伦兹空间上的q-正则算子为例给出新不等式的具体示范。

扫描二维码，阅读英文原文

原文出自 Mathematics

Arnau, R.; Sánchez-Pérez, E.A. Lipschitz Transformations and Maurey-Type Non-Homogeneous Integral Inequalities for Operators on Banach Function Spaces. Mathematics 2023, 11, 4599.