导读

在光学微操纵（如光镊）中，受其开放特性影响，光操控微粒的动力学行为表现出显著的非厄米特性。为应对该非厄米特性在光操纵中带来的挑战，南方科技大学吴紫辉教授（理论）、鲁大为教授（实验）与北京量子信息科学研究院魏世杰助理研究员（理论）提出了一种利用量子计算模拟光操控微粒动力学行为的方法。他们通过量子计算实验，成功仿真了光操控微粒中的奇异点（Exceptional Point）、不稳定复数模态、以及微粒的运动轨迹，为该领域的研究提供了全新的思路与工具。

该成果发表在《Light: Science & Applications》，题为“Solving non-Hermitian physics for optical manipulation on a quantum computer”。南方科技大学博士生樊宇昂、香港科技大学博士后研究员李肖、以及北京量子信息科学研究院助理研究员魏世杰为论文共同第一作者，吴紫辉教授和鲁大为教授为共同通讯作者。

研究背景

近年来，非厄米物理在众多领域引起了广泛关注。其中，奇异点（即本征值与本征态同时发生简并的特殊点）在非厄米系统中的出现，赋予了该类系统独特而奇异的物理特性。最近，非厄米物理的研究更是进一步被引入到光学微操纵系统中。光操纵系统中的非厄米特性主要源于其开放特性：通过光与微粒的相互作用，入射光场能够持续为被操纵微粒注入动能，从而使其呈现出非厄米动力学行为。值得注意的是，受到真空低阻尼环境的影响，这种非厄米动力学行为在真空光操纵中表现得尤为显著。然而，目前用于研究和表征这种非厄米光操控特性的方法却相对有限，这在很大程度上限制了人们对非厄米光操纵微粒，尤其是非厄米真空光操纵的深入理解。

研究亮点

为了应对上述挑战，南方科技大学吴紫辉教授和鲁大为教授课题组开发了基于量子计算的方法，并用于研究非厄米光操控的动力学特性。该研究首先展示了奇异点与不稳定复数模式在单一微粒的光捕获（光镊）系统中的存在。如图1所示，通过将聚焦光场的偏振态从线偏振逐渐过渡为圆偏振，随着聚焦光场中轨道角动量的增加，光捕获系统的非厄米特性也随之增强。在这一相变过程中，研究团队观察到了奇异点与复数模式的存在，其中奇异点标志着稳定模式与不稳定模式之间的临界点。

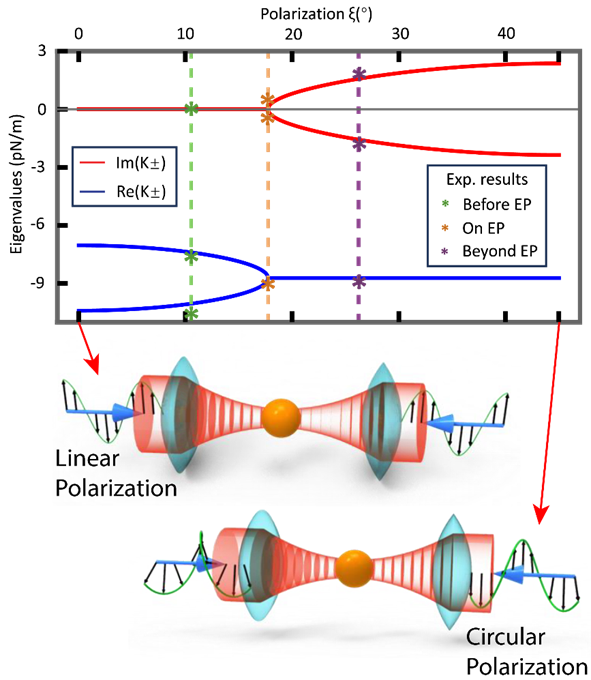
图1. 光操纵单一微粒（光捕获）的奇异点和复数本征模式（理论与量子计算实验）。

研究团队通过量子计算的方法，实验得到了光捕获单一微粒的运动轨迹，这与图1中展示的实数模式（奇异点前）、奇异点模式和复数模式（奇异点后）一一对应。在奇异点之前（图2a和2d），实数本征模式表明微粒以实数本征频率振荡，表现为稳定的光捕获状态。在奇异点处（图2b和2e），简并的本征模式意味着微粒在与该模式垂直的自由度上没有等效的回复力，因此其运动轨迹在该垂直方向上呈现出较大的运动范围。在奇异点之后（图2c和2f），成共轭对出现的复数本征模式中必然包含一个不稳定模式，导致光捕获微粒的运动变得不稳定。这些结果清晰地揭示了奇异点作为非厄米光操控中稳定性分析的关键临界点的重要地位。

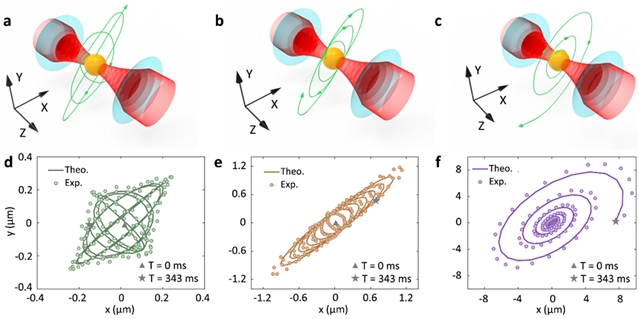
图2. 光捕获单一微粒的运动轨迹（理论与量子计算实验）。（a,d）奇异点前（实数本征模式）；（b,e）奇异点上（本征模式合并）；（c,f）奇异点后（复数本征模式）。

此外，研究团队更是进一步地讨论了光束缚多个微粒的量子计算仿真问题。不同于光捕获，光束缚是另一重要的光操纵工具，主要用于实现对多个微粒的捕获和束缚。光束缚中涉及到更为复杂的光操纵分析，微粒之间的多重光散射所导致的光力也应该被考虑在内。针对被两个平面波（驻波）束缚的球链系统（图3a），研究团队通过引入平面波场强的对称性破缺来逐渐增强该系统的非厄米特性，并观测到奇异点与复数模式的存在（图3b）。并且，针对奇异点前、奇异点上、以及奇异点后的运动轨迹（图3c-e），研究团队也给出了详细的讨论。

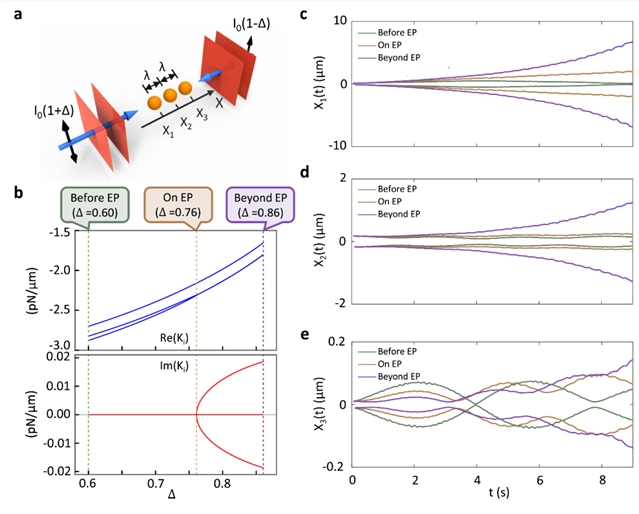
图3. 光束缚多微粒系统的奇异点、复数本征模式、和运动轨迹。（a）利用场强对称性破缺来引入非厄米特性；（b）光束缚多微粒系统的本征模式（出现奇异点和复数本征模式）；（c-e）奇异点前、奇异点上、奇异点后的运动轨迹。

总结展望

本研究展示了量子计算在单个微粒的光捕获（光镊）及多个微粒的光束缚等光操纵系统中的应用。相比于经典计算机上的传统计算方法，本研究奠定了利用量子计算探索大规模非厄米光操纵系统的基础框架，为研究其动力学特性与操控机制提供了新的见解与研究方案。（来源：LightScienceApplications微信公众号）

相关论文信息：https://doi.org/10.1038/s41377-025-01769-2