导读

近日，来自美国加州理工学院的Alireza Marandi团队提出并实验证明了一种基于深度学习的新型光子神经元胞自动机。该成果发表在国际顶尖光学期刊《Light: Science & Applications》上，题为“Deep Learning with Photonic Neural Cellular Automata”，Gordon H.Y. Li为论文第一作者，Alireza Marandi为论文通讯作者。

研究背景

随着深度学习模型在计算机视觉、语言处理以及科学探索等领域的逐步发展，其模型日益复杂，需要更为高效和可扩展的硬件来处理不断增加的计算需求。光子学在深度学习领域中的运用逐渐增多，光子硬件可以实现前所未有的处理速度，且并行性和功效也远超传统电子架构。两者的融合已成为一个非常有潜力的研究领域，可以重新定义神经网路计算的格局。

在传统的深度学习架构中，光子神经网络（PNNs）的主流包括多层感知器(MLPs)和卷积神经网络(CNN)等，但是这些架构的密集连接层一般都需要大量参数，这为光子平台带来了极大的挑战，也使得PNNs难以适应现代深度学习模型的复杂结构，并且在识别未经训练的数据时存在可靠性问题。

为了克服光子学和传统神经网络架构之间的差异，加州理工学院Alireza Marandi团队，提出并实验证明了一种基于神经元胞自动机(NCA)的新型PNN。元胞自动机(CA)是一种由一系列遵循特定更新规则的元胞组成的计算模型，更新规则定义了元胞随着相邻元胞的变化而演变的规律，如图1a所示。与传统的更新规则不同，NCA(如图1b)利用元胞自动机的复杂动态学习技术，实现特定任务所需的更新规则，如再生模式、自分类图像和纹理生成。团队展示的光子神经元胞自动机(PNCA)结合了光子硬件与NCA的优势，实现了自组织图像分类。与以往的PNNs相比，PNCA使用了完全不同的方法来完成计算机视觉任务。此外，由于光子硬件具有固定的权值，因此只需要对局部更新规则进行参数编码。因此PNCA可以实现高效的参数编码解决方案。

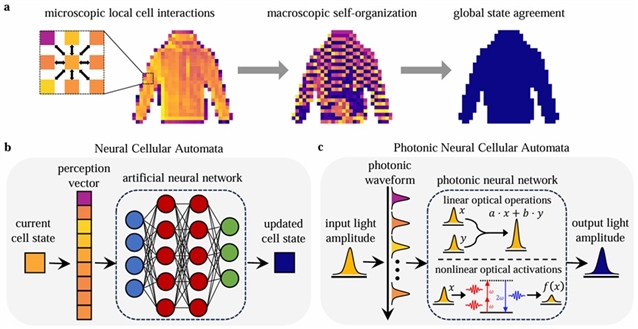
图1. PNCA架构图。

创新研究

PNCA架构

一般PNCA的架构概念如图1所示。对于计算机视觉任务，输入图像中的每个像素都对应于PNCA中的一个元胞。被掩蔽的元胞被定义为死元胞，未被掩蔽的元胞被定义为活元胞。只有活元胞可以被PNCA主动更新，而死元胞只能影响活元胞的更新规则，在其他方面是不变的。元胞的状态根据特定规则进行更新，该规则依赖于元胞附近的m个元胞。例如，图1a显示了元胞与其周围的8个元胞互联、更新示例。在PNCA中，每个元胞对应的光场被分割成m个光路，根据规则更新邻近的m个元胞。PNCA的更新规则由光子硬件编码决定（图1c），它接受m个临近的元胞的输入，并输出下一个元胞状态。对于PNCA来说，最关键的区别在于光子硬件只需要稀疏的互联和足够的参数来编码局部更新规则，通常比MLP和CNN的架构中的参数少几个数量级，即PNCA架构可以使用相对较少的参数实现更大更复杂的任务。

PNCA实验

研究团队使用时分复用系统和商业光纤元件对一个简单的PNCA进行了实验验证，如图2所示。每个元胞状态由固定重复频率的锁模激光器产生的激光脉冲振幅给出，通过一维网格对二维图像进行逐帧扫描，给每个元胞赋予一个初始状态。这样，每个元胞之间都具有一个时间差。因此，可以使用时间延迟线使不同位置的元胞交互。使用电光调制器(EOM)设置代表元胞状态的脉冲幅度/相位，然后将脉冲在3条相对延迟为T1和T2的光学延迟线之间分光，以实现如图2b所示的3-元胞更新。在这个简单的例子中，局部更新规则由单个感知器神经元编码，如图2c所示，它由一个线性点积函数和一个非线性激活函数组成。点积是通过光学延迟线的相干干涉来实现的，每个延迟线都配备了一个可变的光学衰减器(VOA)来编程所需的权重。非线性激活是在铌酸锂波导中实现的，产生了如图2d所示的类S型函数。从而实现了全光的局部更新计算规则。总体而言，局部更新规则只包含3个可编程参数，但仍然可以执行复杂的任务。最后，使用现场可编程门阵列(FPGA)上的光电探测器测量元胞状态，用于下一次迭代。

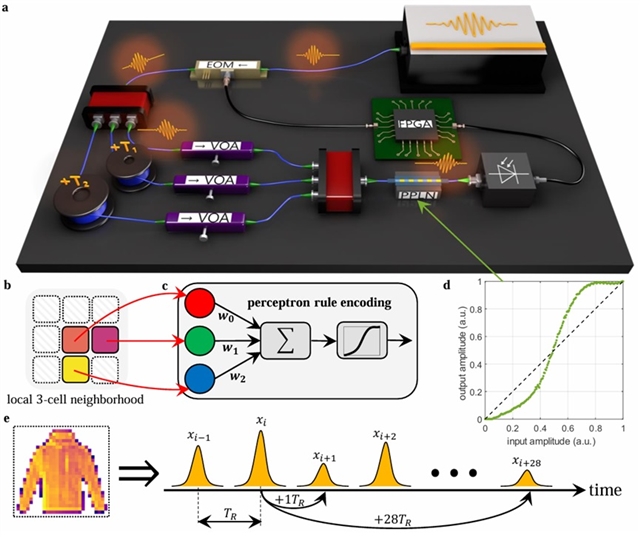
图2. PNCA实验验证装置图。

由于元胞状态的自组织特性，PNCA架构的一个关键优势是具有抗噪声的鲁棒性。团队使用200张测试图像来描述抗噪声的鲁棒性。这些图像中活元胞的预期和测量的振幅见图3。我们的系统中实现的误差平均值和标准差与传统的光子神经网络中达到的效果相当。

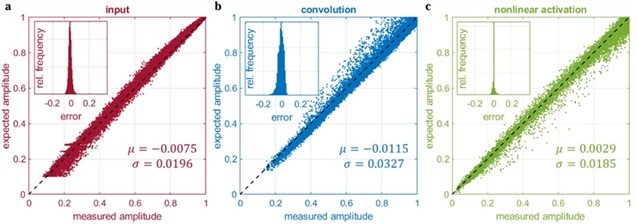
图3. PNCA工作的噪声和误差测试。

自组织图像分类

使用28×28像素灰度图像的fashion-MNIST数据集训练PNCA，进行二进制图像分类。图4a显示了PNCA如何对运动鞋和裤子的图像进行分类。每个输入图像在PNCA中迭代t = 21个时间步长，这足以使元胞达到近似的全局一致。

在无噪声的理想PNCA模型中进行数字化训练。理想模型的混淆矩阵如图4b所示，最终的测试精度为99.4%。然后在模型加入模拟高斯噪声进行测试，噪声模型的混淆矩阵如图4c所示，其最终测试精度为97.7%。训练后的模型参数通过适当调整可变的光学衰减器(VOAs)在实验PNCA中实现。用200幅图像测试的实验结果的混淆矩阵如图4d所示，最终测试准确率为98.0%。这一实验测试精度与模拟噪声模型非常接近，这表明PNCA按照预期运行。

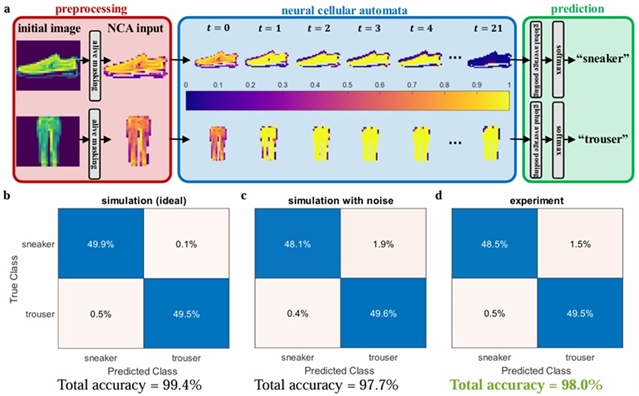
图4. 时尚类物品二值图像分类实验结果。

分布外数据测试

传统神经网络无法推广到预测训练数据分布以外的数据，而NCA使用所有活性元胞的平均状态值作为测量不确定度来解决这一问题。团队通过实验证明了这一点，使用在运动鞋和裤子图像上训练的PNCA，对手提包图像进行分类，这是PNCA在训练中没有接触过的一种物品类别。运动鞋、裤子和手提包类的活元胞平均值分布如图5a所示。结果表明，初始状态的活性元胞无法区分三类物品。通过后续在训练中学习迭代，PNCA成功分离出运动鞋和裤子的分布，最终活元胞平均值分别为0.1743和0.8742，如图5b所示。在这种情况下，活元胞平均值在0 ~ 1之间的差异表示预测的不确定性。然而，手提包测试图像的最终活元胞平均值为0.5682，接近0.5，这意味着元胞没有达成全局一致。这表明PNCA可以使用活元胞平均值作为不确定性参数，并用于检测分布外数据。

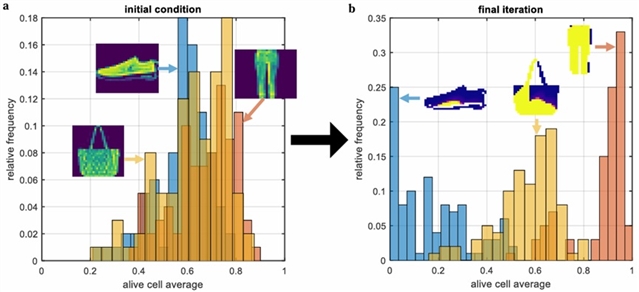
图5. 分布外数据识别实验结果。

总结与展望

未来，PNCA架构也可以与更先进的PNN硬件结合，使用更多的神经元/参数来表示局部更新规则。更多的神经元/参数可以实现更复杂的任务和更高的分类精度，而硬件复杂度远低于其他神经网络架构。此外，与MLPs或CNNs相比，高效的PNCA模型编码所需的参数减少了几个数量级。因此，本研究工作为推进PNCA的光子深度学习指明了道路，并为下一代光子计算机铺平了道路。（来源：LightScienceApplications微信公众号）

相关论文信息：https://doi.org/10.1038/s41377-024-01651-7