|
|
|
|
|
FEM 公共卫生事件下的具有运输容量限制条件的城市轨道交通线网节能开行设计 |
|
|
论文标题:Toward energy-efficient urban rail transit with capacity constraints under a public health emergency
期刊:Frontiers of Engineering Management
作者:Kang HUANG, Feixiong LIAO, Soora RASOULI, Ziyou GAO
发表时间:15 Dec 2024
DOI:10.1007/s42524-024-3088-9
微信链接:点击此处阅读微信文章
作者:黄康1,2,3, 廖飞雄2, Soora RASOULI2, 高自友3
单位:
1. 能源、环境、社会综合研究中心,科学与工程学院,格罗宁根大学,格罗宁根市,荷兰
2. 城市规划与交通管理研究组,埃因霍温理工大学,埃因霍温市,荷兰
3. 系统科学学院,北京交通大学,北京市,中国
引用:
Kang HUANG, Feixiong LIAO, Soora RASOULI, Ziyou GAO. Toward energy-efficient urban rail transit with capacity constraints under a public health emergency. Front. Eng, 2024, 11(4): 645–660 https://doi.org/10.1007/s42524-024-3088-9
文章链接:
https://journal.hep.com.cn/fem/EN/10.1007/s42524-024-3088-9
https://link.springer.com/article/10.1007/s42524-024-3088-9
导语:城市轨道交通(URT)承担着在封闭的公共空间内运送大量乘客的重要任务,因此在公共卫生突发事件中很容易扩散传播传染病。本研究提出了一种决策支持模型,该模型结合了乘客流量和列车满载率方面的运营控制策略,旨在提高紧急情况下城市轨道交通网络的能耗表现。在设想中的城市轨道交通系统中,乘客应遵循推荐路径,并接受细化的路径流量控制,而列车的满载率则受到约束,以促进保持社交距离。以2021年底中国西安市爆发COVID-19事件为例,本文对决策支持模型的有效性进行了评估。结果表明,与粗放式管理相比,对客流和风险区域进行有针对性的精准管控可进一步提高节能和乘客出行的便利性。
关键词:城市轨道交通;突发公共卫生事件;精准管控;列车满载率;节能
1.导言
公共交通是日常大量乘客出行的主要方式之一,其人均能耗远低于私家车(Xie 等,2021年)。然而,在公共卫生突发事件(如COVID-19)期间,公共交通的乘客需求通常会减少,并转向私家车,这可能会导致更多的能源消耗和排放 (de Palma 等,2022 年)。公共卫生突发事件发生时,人们的出行流动性是传染病传播的主要渠道之一。在公共卫生突发事件期间,在没有任何控制措施或政策的公共交通工具上,乘客通常很难始终保持建议的社交距离。因此,在封闭的公共交通车辆中,不可避免的接触(即使比例很小)也可能导致传染(Harris,2020年)。因此,公共交通的客流控制(PFC)对于遏制突发公共卫生事件的传播和负面影响至关重要 (Zhang 等,2022 年;Sun 等,2023年)。在后大流行时代,大流行可能会在小范围内反复爆发,或成为一种季节性传染病,可能会有不同的变种。当COVID-19 显示出较低的健康风险时,应逐步恢复公共交通服务和连通性,因为它们是人们经济生活的推动力(Zeng 等,2021年;Luo等,2023年) 。一旦公共交通无法很好地过渡到 "后疫情公共交通时代",乘客需求与交通服务供给之间可能会出现严重的不匹配,这不利于整个交通系统的公交导向发展和碳减排(Tirachini & Cats,2020年)。例如,与运营商减少城市轨道交通(URT)线路的发车频次或部分关闭以控制蔓延相反,乘客希望有更高的发车频次次和更多的运营线路,以保持社交距离 (Elias & Zatmeh-Kanj, 2021年)。鉴于需求与供给之间不可或缺的互动关系,有必要为后疫情时代的城市轨道交通服务制定有效的控制措施,以协调大量反弹的出行需求和防止疫情蔓延(Zhou & Koutsopoulos, 2021年) 。
城市轨道交通是主要的公共交通方式之一,承担着城市居民大量的日常出行需求,可有效减少道路交通拥堵和碳排放(Pan 等,2018;Zhang 等,2022年)。城市轨道交通系统采取了一系列措施 (Jia 等,2021年) ,被称为突发公共卫生事件的标准操作流程,例如,预先部署医疗物资和设备、确定紧急情况类别和风险等级、分析具体操作措施、实施有效措施 (Borjigin 等,2023 年)。一方面,城市轨道交通与高运营成本和能源消耗有关 (Huang 等,2017年)。例如,北京轨道交通集团公司,在2020年消耗了超过20亿千瓦时的电量,成为北京市耗电最多的公司(Lv等, 2019年)。另一方面,在城市轨道交通列车内保持一定的满载率,否则预计会很拥挤,这也是防止大流行病传播的有效措施。列车满载率是缓和乘客之间社交距离的有效指标。因此,为了提供必要的社交距离条件,应在保持尽可能高的列车运能利用率的同时,实施客流控制以实现乘客的时空再分配。目前很少有研究考虑多线路城市轨道交通网络的节能目标以及客流与时刻表计划的同步性(Kang 等,2020年)。因此,只要城市轨道交通没有完全关闭,就应考虑在公共卫生紧急状态下的运行能耗问题。
为协助公共卫生突发事件下的城市轨道交通运营管理,我们提出了一种节能开行设计决策支持模型,其中包含客流量和列车容量利用率控制。每条城市轨道交通线路的列车发车频次和乘客路径分配是决策变量。该决策支持模型旨在最大限度地减少能源消耗,同时控制轨道上的列车满载率以及乘客更换路径所带来的不便。节能是一个合适的目标,原因包含两方面。首先,能源消耗与运营 成本密切相关,因此可将其视为运营成本的替代目标,许多节能优化模型都采用了这一目标(Canca & Zarzo, 2017年; Yang等, 2023年 ; Huang等, 2023年)。其次,在突发公共事件成为新常态后,应将运营能耗表现恢复为常规目标,这不同于突发公共事件开始阶段其他目标可能具有较高优先级的情况 (Gao & Yang, 2019年; Wang等, 2017年)。对于那些需要改变路径的乘客,在路径生成的预处理中,新路径与原路径(未实施控制时)相比的额外旅行时间被隐含地限制了。这样一来,乘客方面选择旅行时间最短路径的目标就得到了部分考虑。更确切地说,假设乘客到达火车站的时间(或进站率)由设想中的数字预约系统控制,那么乘客的时空分布将在所需的列车容量利用率下得到优化。考虑到公共卫生突发事件下的不同风险等级,轨道上的列车满载率可以自适应设置。考虑到突发事件的地理分布,列车满载率的 约束条件 可以针对特定风险等级的区域。据我们所知,这是首次在考虑城市轨道交通节能和乘客便利性的情况下,对客流控制进行研究,以防止公共卫生突发事件的蔓延。本文提出的决策支持模型以2021年底西安市爆发COVID-19疫情为真实时间线进行了测试。结果表明,针对风险区域的有针对性的客流控制能够有效地促进社会隔离和节约能源,同时将乘客的不便控制在合理范围内。考虑到受客流控制影响的OD对数所显示的能源消耗和乘客不便之间的权衡,决策支持模型框架讨论了大流行病不同阶段的几种控制策略。
本文余下部分的结构如下。第2节以COVID-19为特例,阐述了公共卫生突发事件下 城市轨道交通网络中利用客流控制进行节能开行设计的问题。第3节建立了节能开行设计的决策支持模型,其中介绍了假设、约束条件和目标。第4节评估了建议的决策支持模型的有效性,第5节讨论了政策影响、结论和进一步的研究方向。
2.城市轨道交通网络中的客流控制和节能
为保证列车车厢内的社交距离,会降低运力。例如,根据中国交通运输部《客运枢纽及车辆 COVID-19 分区分级控制指导意见》,应严格控制高、中风险区列车满载率。调整乘客在时空上的分布,可以要求乘客在乘车前预约。例如,北京市自 2020 年起实施了 "地铁预约"制度,以控制进站率。首先,乘客需要预约出发时间,如图1(a)所示。例如,5月16日的乘客只能预约第二天的行程。如图1(b)所示,乘客的手机会收到一个二维码和指定的闸机入口,有效期为10分钟。如图 1(c)所示,他们可以使用二维码在指定闸口进入城市轨道交通,并在站台等候,同时拉开满载率。最后,乘客上车并保持满载率(图1(d))。根据相关报告,相比之下,乘客每次出行平均可节省3.5分钟。在没有预约系统的情况下,57%的人在上车前会调整发车时间以节省等待时间 (Wang等, 2021年)。如果没有这种预约系统和流量控制,车站(通常是换乘站)和相连路段可能会人满为患 (Guo 等,2020年)。因此,客流控制(或规范路径选择)应与受限制的列车容量利用率相结合。不同区段的风险等级可定义为高、中、低等,因此应针对不同区段实施专门的列车容量利用率。
从运营者的角度来看,为了提供利用率较低的服务以降低感染风险并适应不同的乘客需求,列车发车频次是直接的决策变量(Ning 等,2018年)。作为运营成本最小化与环境负面影响最小化的结合目标,能耗表现最大化(或能耗最小化)是一个相关的运营目标(Zhou 等,2023年)。因此,拟议决策支持模型的目标是在满足列车满载率约束条件的同时,最大限度地降低能耗。如图2所示,决策支持模型有三组输入。首先,对于 客流控制,基于配额的预约模块划定了允许到达的最大乘客人数。在生成替代路径时,要剔除较长的绕行路径(如超过最短旅行时间的1.5倍),以避免乘客旅行时间过长(Huang & Liao,2023)。通过预约界面(图1),向乘客推荐路线和进入点。其次,指定风险等级、时间段和受影响区域,以确定规定的利用率。第三,城市轨道交通运营参数包括速度曲线、列车队规模和运营周期,这些参数共同决定了时刻表。通过这些输入,可以在优化模块中根据能耗表现目标确定所有城市轨道交通线路的乘客路径分配和列车频率,从而进行开行设计。可以计算出每条路径和轨道上的乘客量,从而找出轨道或车站的瓶颈,确定列车发车频次。

图 1. 北京城市轨道交通预约系统示意图
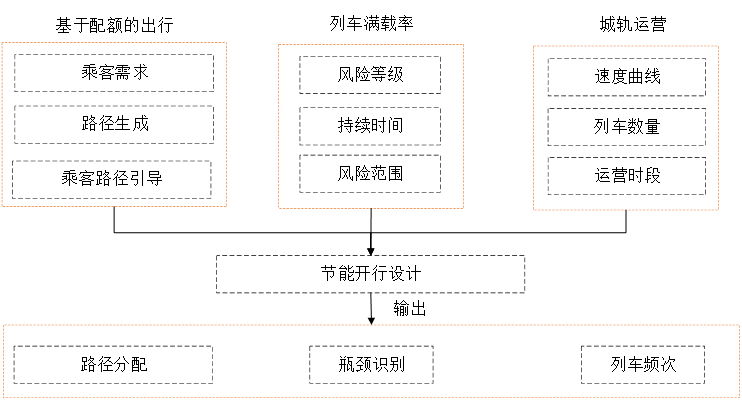
图2. 应对突发公共卫生事件的决策支持模型
3.决策支持模型
本节将介绍一个用于城市轨道交通网络节能开行设计的决策支持模型。该模型框架包含公共卫生突发事件下的客流控制和列车容量利用率。下文介绍了该模型的主要假设、约束条件和节能目标。
假设条件:
根据第 2 节中的问题描述,决策支持模型有以下假设。首先,在时间跨度相对较长的突发公共卫生事件(如COVID-19)中,时刻表是并行统一安排的。时刻表主要涉及战术层面开行设计阶段的列车发车频次 (Mo等, 2019年)。没有考虑运营层面更详细的时刻表。其次,规划期内的乘客需求是确定的,由预约系统提供。预约系统类似于长途汽车或火车的售票系统。城市轨道交通开行设计需要运送来自预约系统的所有(时间上)均匀分布的乘客需求。因此,该模型可在基于频率的城市轨道交通的静态背景下构建。第三,如果没有客流控制,乘客会选择广义成本最小的路径。一条路径的广义成本可能涉及几个部分,即在第一个站台的等候时间、换乘时间(如果有的话,包括步行和等候时间)、轨道上的运行时间、在站台的停留时间以及票价。需要注意的是,这些成本组成部分系数的估算或校准不在本研究范围之内。第四,在突发公共卫生事件中,乘客会严格遵守运营者推荐的路径(服从率为100%),而这不一定是成本最低的路径。
约束条件:
节能开行设计决策支持模型涉及三组约束条件,分别是乘客路径分配、列车容量利用率和客流控制强度。
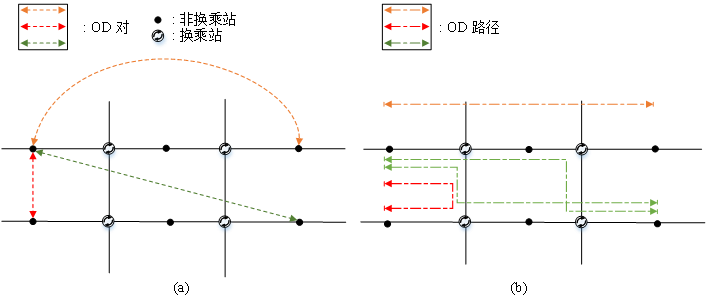
图3. 不同OD对的路径分配示意图
需要换乘到达目的地的乘客可能有不止一条备选路径,备选路径的存在为客流控制提供了可能性。乘客路径分配将决定了线路l的运行区间t上的客流量qlt。为了乘客是否存在路径选择,将乘客OD对分为两类,对于那些只有一条备选路径的OD对,乘客没有额外的路径选择,直接被分配到路径上,其在规划期间分配到运行区间上的客流量,qlt0,可预先计算。对于具有多个备选路径的OD对,相应的OD对集合U1将决定每个运行区间的总客流量qlt。例如,在图3(a)中,线网中有三个代表性的OD对,由四条城市轨道交通 线路(两条垂直黑线和两条水平黑线)组成。橙色虚线表示的O和D在同一条城市轨道交通线上的OD对到图3(b)中,橙色OD对之间存在直达列车并且只有一条备选路径。红色虚线表示OD对其O和D在的不同城市轨道交通线路上,在淘汰迂回的备选路径后,也只有一条备选路径。绿色虚线表示的OD对需要换乘,并且有两条路径成本相当的备选路径。路径–区间流量守恒可以表示为公式(1)-(3)。公式(1)表示运行区间流量由两类OD对分配的流量加和。
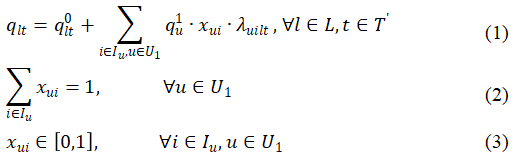
其中l和L是运营线路索引和集合。T是城市轨道交通线网中的一组重要运行区间。是有不止一条备选路径OD对u的对应的乘客需求。i和Iu为属于OD对u的路径索引和路径集合。0-1参数:λuilt=1当线路l的站台p属于路径r;否则λuilt=0。xui表示OD对u分配给路径i的乘客比例,每个OD对u对应所有路径i的比例之和为1,如公式(2),同时如公式(3),路径分配比例xui属于0到1之间的范围。
其次,列车满载率受制于预期的社交距离。对于每条城轨线路,l的列车发车频次 fl 由最大客流量的轨道决定,并要求运送所有乘客。最大乘客量qlmax 是公式(4)中所有轨道乘客量的上限。作为路径流量控制的结果,列车满载率影响并决定了列车中的社交距离水平。需要注意的是,列车中的满载率不同于开放空间中的满载率(例如,标准距离为 1 米或 1.5 米)。在公式(5)中,列车应在给定的列车容量利用率φ下容纳所有轨道上的乘客。根据突发公共卫生事件所处的不同阶段,强制性列车满载率φ可设定为不同的水平。例如,φ=0意味着关闭轨道交通系统;如果0<φ<1,则实施客流控制;1<φ≤φmax 指的是超载,其中φ max 是正常运营中出于安全考虑而允许的最大列车容量利用率。考虑到城市轨道交通系统的安全和容量,每条线路的频率都有一个上限约束,f lmax ,见式(6)。
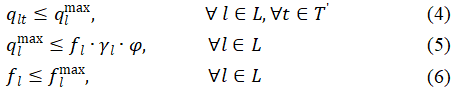
其中γl 是列车在l 线路上的满载运输能力。
第三,客流控制的强度应受到限制,以避免给乘客带来过多不便。客流控制需要考虑运营成本和乘客改变其通常的最小成本路径所带来的不便。让α表示乘客可以从最小成本路径转向其他路径最大OD对比例。由于放弃最小成本路径会给乘客带来不便和额外成本,因此 α 反映了客流控制的强度。改变路径的OD对规模受公式(7)约束,其中y_u 为二元变量,yu=1 ,如果有OD对u的乘客将路径从最小成本路径改为其他路径;否则,yu=0 。xu1 为OD对u的乘客选择最小成本路径的比例。xu1和yu的关系式描述为公式 (8)。约束条件(6)-(7)可转化为乘客从最低成本路径转向其他路径的约束条件。
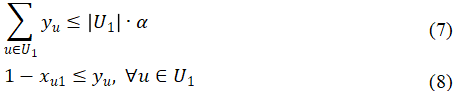
城市轨道交通的节能目标
城市轨道交通系统牵引能耗包含加载空载列车和乘客两部分重量因素。让El1 和El2 分别表示 l 线路所有轨道的空载列车和乘客重量的分解能耗。总能耗可通过 ∑(l∈L)flEl1 和 ∑ (l∈L) flEl2 两部分相加计算得出。空车能耗为 l 线路所有轨道的能耗总和,如式 (9),其中elt0 为 l 线路轨道区间 t 上空车的基本能耗。根据乘客重量和空载列车能耗之间的稳定关系,我们根据空载列车能耗和两部分能耗的比值θ计算出总能耗,如式(10)所示。需要注意的是,θ与列车满载率φ有关。例如,在列车容量利用率为φ=1(满载)的情况下,∑ (l∈L) flEl2 与 ∑(l∈L)flEl1 之间的比率约为1:3(Huang 等,2021 年)。乘客装载量(或列车满载率)越大,θ 越大。
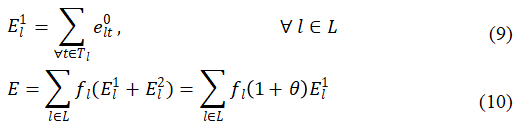
决策变量 xui 是客流控制的目标和预约系统的结果,而 fl 受列车容量利用率约束的影响决定了总能耗。能耗最小化模型目标概括为

该模型为混合整数线性规划(MILP),变量和约束条件的规模在可控范围内均可求解。求解器(如Gurobi)可在可接受的计算时间内找到精确解。该模型确定了城市轨道交通线网的列车发车频次,而无需修改各轨道的运行时间和停留时间等时刻表要素,这使得城市轨道交通网络中的最小成本路径在很大程度上保持不变。此外,在突发公共卫生事件中,乘客更愿意选择OD可达性,而不是寻求广义旅行成本最小的路径。该决策支持模型为评估公共卫生突发事件下的城市轨道交通时刻表提供了宏观参数,如与发车频次相关的平均等候时间和换乘时间。为探索微观效果(通常在正常运营中)对精确等待时间和换乘时间的影响,模型应扩展更多的时刻表要素决策变量以及时刻表与乘客路径行为之间的反馈(Huang 等,2021年)
关于模型复杂性的解释
表1列出了决策支持模型中变量和约束条件的数量。决定模型复杂度的主要因素有四个:(1) |U1 | 中的OD对数(2)备选路径的数量,∑(∀u∈U1)|Iu| ,这与OD对的规模有关;(3) 关键轨道集的大小|T|;(4) 城市轨道交通网络中线路的数量|L|。在规模较大的城市轨道交通网络中,如果不做任何简化,模型就是大规模混合整数线性规划。为了缩小变量规模,节省计算时间,可以从两个方面进行简化。首先,在对风险区域进行有针对性的管理和控制的情况下,一条关键轨道可能是瓶颈,可用来代表在一条路径上没有转移机会的多条轨道。|T| 可能只是原始轨道的一小部分。其次,路径不覆盖任何关键轨道的OD对可以忽略。在简化的城市轨道交通网络中,路径分配重叠的OD对也可合并为一个OD对,并将乘客需求汇总。在实际应用中,U1的规模可能只是原始OD对的一小部分。有了这些简化,决策支持模型中的优化模块就可以高效地求解出精确的最优解。
表1. 模型中变量和约束条件的数量(|·|为集合的大小)

关于目标管理的说明:
按照突发公共卫生事件的标准操作程序,城市轨道交通运营者将启动乘客路径流量控制,以支持有针对性的管理。针对分区风险等级,客流路径流量控制的强度包括通过预约系统允许进入城市轨道交通系统的乘客总数、轨道上的列车容量利用率(φ)和线路上的列车发车频次(fl)。例如,在上述 COVID-19 的分区分级防控指引中,高风险区和中风险区的列车满载率应分别设定为0.5和0.7。对于专门的客流控制政策,即定向管理,应根据风险等级区分区域,以避免不必要的负面影响。根据中国国务院文件[冠状病毒肺炎预防和控制计划],低风险区对列车运能利用率没有限制,但要求佩戴口罩。相对而言,高风险区的列车运能利用率最低。当列车从低风险区开往高风险区时,客流控制会将更多乘客从最低成本路径转移到其他路径,以满足列车满载率,高风险区的上车率也会降低。因此,应将公式(4)-(5)替换为公式(12)-(13)。
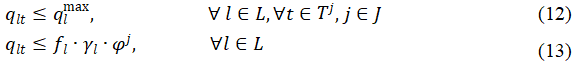
其中j和J为风险等级和风险等级集,J={j|j=1,2,..N}, Tj 为 j 风险等级区域内的关键轨道集 ,φ j为 j 风险等级区域内紧急情况下的列车满载率 ,N 为最大风险等级。
总之,用于节能开行设计的决策支持模型可为多种目的提供最佳解决方案,如在城市轨道交通网络中实现节能、列车容量利用率以保证社交距离的和客流控制。
4.法规和政策层面的挑战与进展
该决策支持模型被应用于突发公共卫生事件(即COVID-19)的实际案例研究,以证明其有效性。案例研究地区西安市是陕西省省会,也是中国西北地区最发达的地区 (Yin 等,2021) ,拥有一个中等规模的城市轨道交通网络,拓扑结构呈方形。在本案例研究中,共有4条线路、94个车站(双向站台分别为38、42、52和56个),总里程为158公里。关于188个站台和180条轨道的详细信息,可见Huang等人,2021的附录文件。城市轨道交通网络的最大列车编组为24列,每列列车满载乘客1762人。由于许多OD对的路径选择有重叠的路径分配,原始城市轨道交通网络可从图4(a) 简化为图4(b)。简化后的网络由换乘站附近的代表性轨道组成,共有26个车站和44条轨道。对于1-4 号线,双向轨道的数量分别减少为10、12、10和12。每个OD对的备选路径由 k 最小成本路径算法生成,本城市轨道交通网络选择 k=3。旅行时间大于最小成本路径旅行时间1.5倍的路径将被排除。在676个OD对中,有多于一条备选路径的OD对为337对。乘客需求量来自2021年 COVID-19 第二阶段上午 10:00 至11:00 期间的自动收费系统 (AFC),该数据应为设想中的预约系统数据。在非高峰时段,上下行方向的每小时乘客需求相对平均,因此选择一小时的时间范围进行分析。在非高峰时段,乘客出行总量为141567人次,77%的乘客出行有不止一条可供选择的路径。对于仅有一条路径可供选择的OD对,乘客需求(23% 的乘客人次)直接分配给单条路径。图5显示了各条轨道的客流量。在商业区和设施集中的城市轨道交通线路的中间部分,乘客量较大,并出现高峰客流。上下行方向的每小时客流量几乎对称。在现有时刻表下,1号线至4号线空车从起点站台至终点站台的能耗(El1)分别为712.5千瓦时、792.5千瓦时、1063 千瓦时和1217.5千瓦时。
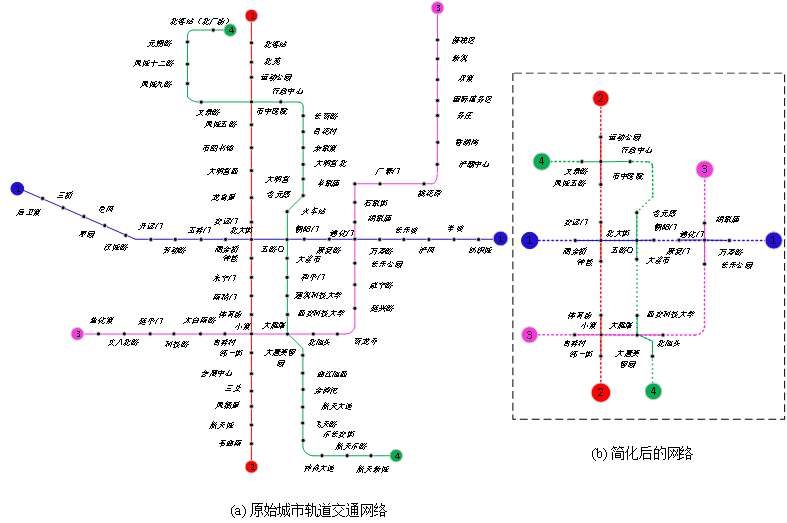
图4. 西安轨道交通网络示意图
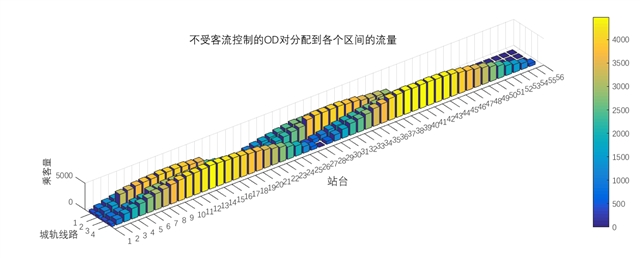
图5. 只有一条备选路径的OD分配到区间的客流量
案例研究基于2021年底西安市爆发COVID-19的真实时间线。2021年12月15日,发现首批确诊病例。次日,经过流行病学调查,多个区域被定义为中危区域。发现了更多确诊病例,其行踪覆盖了更多区域。2021年12月19日,扩大了风险区的范围,增加了高风险区。在大约一个半月后,直到14天内没有再发现确诊病例,风险区域才被取消。为展示拟议模型框架的有效性,我们开发了两个案例。案例1考虑了一种情况,即各区的使用率设置一致,以代表整个城市的广泛管理 (∀t∈T)。案例2则用于考察φ对区域的影响,以体现有针对性的管理。该模型由Yalmip+Gurobi在个人电脑(三星24G内存和英特尔酷睿i7-8550UCPU)上求解,计算时间约为5秒。
案例1:固定的列车运行能力利用率
乘客重量与空车能耗之间的比率θ与列车满载率φ有关。在计算总能耗时,θ和φ之间的一般关系假定为θ=φ/3。基于不限制客流控制强度的优化模块(α=100%),不同φ客流控制 优化方案如表2所示。为便于比较,表2还显示了无客流控制的原始时刻表(所有乘客都选择旅行时间最短的路径)的能耗表现。可以看出,当列车运行能力利用率φ≤0.7 时,考虑到车队规模,没有客流控制的列车运行能力甚至无法满足乘客需求。然而,有了客流控制后,情况就得到了改善。与没有任何路径流量控制的情况相比,所有轨道的客流控制能耗降低了约36%。如图6所示,如果实施 客流控制,在列车容量利用率的限制下,各条线路的列车发车频次在所有情况下都会减少。综合来看,客流控制 可降低列车频率和能耗。

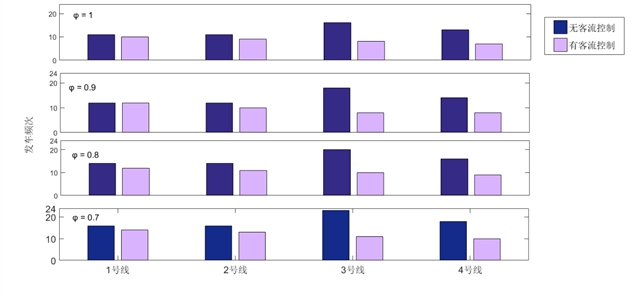
图6. 不同列车满载率下列车频率对比
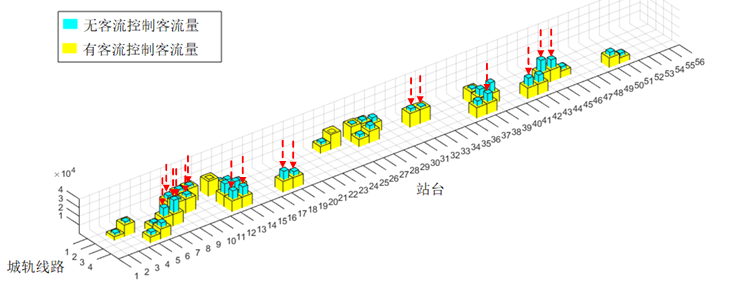
图7. 有无客流控制的区间客流量比较
列车发车频次由轨道上的客流量决定。以φ=0.7为例,有客流控制的主要轨道的乘客量如图7所示,其中大部分轨道的乘客量低于无路径流量控制的情况。虽然部分轨道的乘客量较高,但轨道上的乘客量分布较为均匀。因此,客流控制 可以有效降低各条线路的高峰客流量。可以看出,关键轨道总是包括客流量最大的轨道,这些轨道被认为是城市轨道交通线路的瓶颈(图7中红色箭头所示)。结果还表明,关键轨道的选择是充分和有效的。
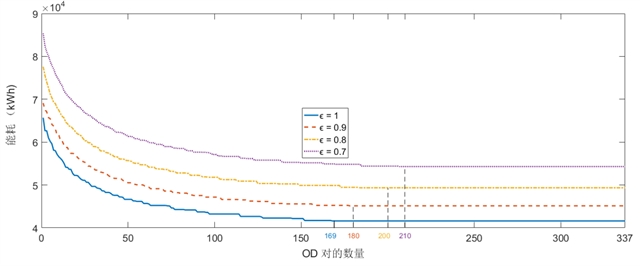
(a)满载率0.7≤φ≤1时能耗随受客流控制影响的OD对数量变化
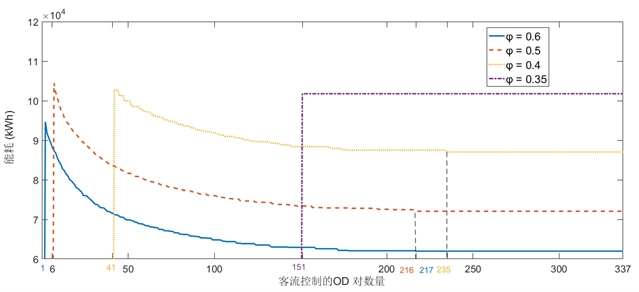
(b)满载率0.35≤φ≤0.6时能耗随受客流控制影响的OD对数量变化
图8. 受客流控制影响的OD对数量对能耗的影响
受客流控制影响的OD对比例及客流控制强度会影响最终能耗。值得注意的是,控制参数α等于受客流控制影响的OD对的允许比例除以OD对总数。当α=50%、30% 和 10% 时,受客流控制影响的OD对的允许规模分别为168、101和34。例如,受客流控制影响的总能耗如图 8(a)所示。当 0.7≤φ≤1 时,随着允许的OD对从最小成本路径转移到其他路径的数量增加,能源消耗 会减少。在列车容量利用率φ=1、0.9、0.8和0.7 的情况下,允许的最小OD对数分别为168、178、184和207。列车容量利用率越严格(越小),需要将客流从最小成本路径转移到其他路径的OD对数就越多。因此,乘客改变路径的不便程度会随着能耗的降低而增加。当0.35≤φ≤0.6时,在没有客流控制的情况下,列车容量不足以产生可行的解决方案。如图 8(b)所示,当α=0时,解决方案不可行。当允许更多的OD对进行客流控制时,可以产生可行的解决方案(例如,φ=0.6,0.5,0.4,0.35,分别为1、6、41、151)。当列车容量利用率较低时,OD对数量的下限较大。
案例 2:基于风险等级不同区段的列车运行能力利用率约束
2021年,COVID-19在西安市的爆发分为两个阶段。如图9所示,在第一阶段,橙色方框内有两个中度风险区,包括8条重要轨道。随着疫情的蔓延和确诊病例的增加,这两个中风险区升级为红色方框中的高风险区。同时,还确定了两个中度风险区,共四个轨道。第二阶段疫情的严重程度高于第一阶段。与风险区相连的轨道要求列车运能利用率较低。高风险区和中风险区的列车运能利用率分别定为0.5 和0.7。
根据决策支持模型,第一阶段各条线路的能耗和列车发车频次见表3。如果将整个城市定义为没有针对性管理的中等风险区域,能耗和列车发车频次都较大。以目标区为中心,在没有客流控制的情况下,总能耗为68571.89 kWh,与整个城市设定为中等风险相比,减少了 20.86%(即(86646.12-68571.89)/86646.12)。同时,通过客流控制,能耗可进一步降低至40330.47 kWh,与全市设置中等风险相比,降低了25.73%(或(54298.97-40330.47)/54298.97)。因此,为了节约能源,提高运输能力,减少乘客路径分配的不便,有必要对风险区域进行客流控制和有针对性的管理。
图10显示了不同控制策略下1-4号线关键轨道区间的乘客量。通过将整个城市(城市轨道交通网络)的所有关键轨道设置为中等风险区(φ=0.7),这些轨道上使用客流控制的乘客量总是低于未使用客流控制的乘客量。从2号线和3号线可以看出,属于目标风险区(粉色矩形)的关键轨道上的乘客量最低。因此,通过有针对性的客流管理,这样,风险区的乘客量可以减少,而不会影响非风险区(即1号线和4号线的轨道)的乘客。
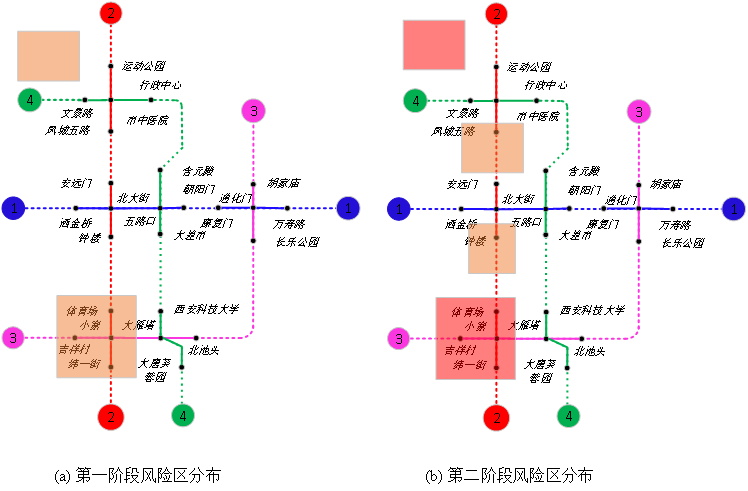
图9. 2021年12月西安新冠疫情(COVID-19)的风险区地理分布
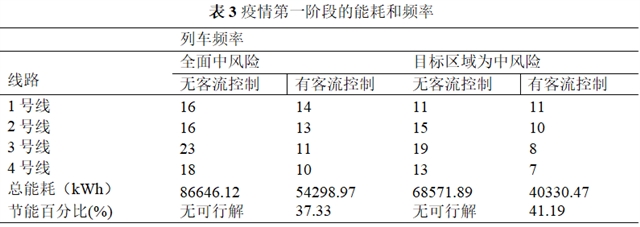
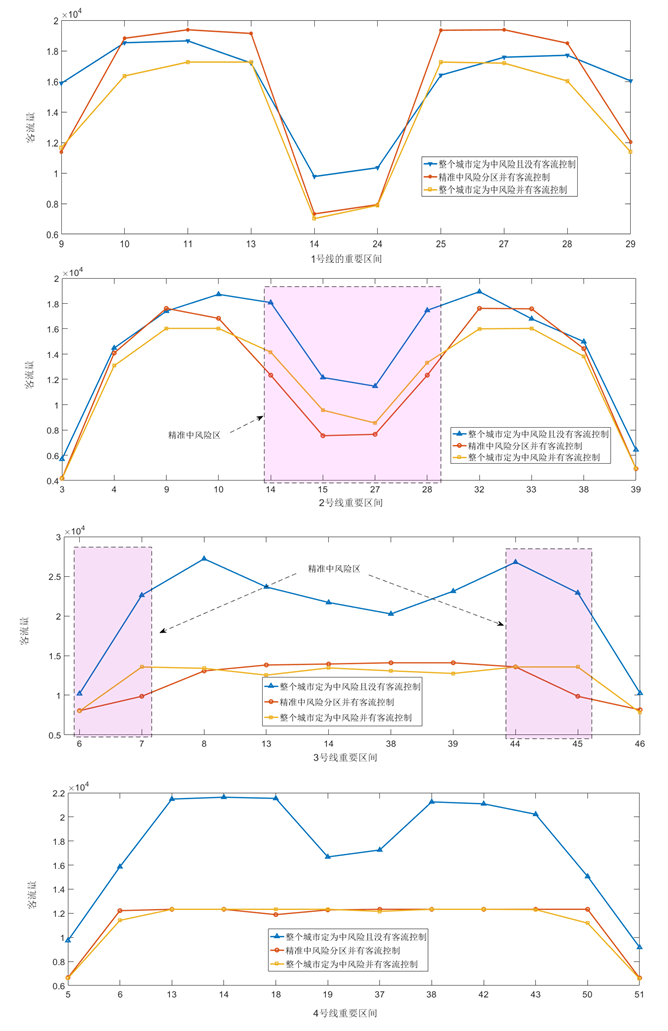
图10. 客流控制对区段乘客量的影响
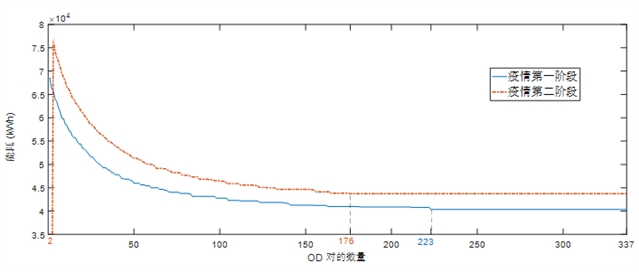
图11. 疫情两个阶段受客流控制影响的OD对数量对能耗的影响
在疫情第二阶段,如果只考虑风险区域的约束条件,则没有客流控制的可行方案。在对风险区域进行有针对性的管理后,能耗为43719.39千瓦时,与对整个城市设置高风险相比,能耗降低了28.34%。如图11所示,在大流行的两个阶段,能耗随受客流控制影响的允许OD对数量的变化而变化。在这两个阶段,需要将客流从最小成本路径转移到其他路径的最小OD对数分别为223和176。当第二阶段允许客流控制的OD对规模小于2时,没有可行的解决方案。在出行需求和客流控制相同的情况下,风险区越多,能耗越高。
总之,对于类似COVID-19这样的突发公共卫生事件,考虑到社交距离的列车满载率,决策支持模型可以在城市轨道交通网络中找到最优的开行设计和乘客路径分配。客流控制 带来的能源消耗和乘客不便之间存在权衡。对风险区域进行有针对性的客流管理,而不是对整个城市进行粗放式管理,可以有效降低能耗和乘客因改变常规路径而带来的不便。
5.讨论和结论
根据案例研究的结果,讨论了大流行病不同阶段的几种控制政策。此外,还讨论了主要结论和未来研究工作的可能性。
5.1 政策影响
根据第4节的结果,轨道上的列车容量利用率、风险区域覆盖率和客流控制强度对城市轨道交通网络的能耗和运输能力都有影响。因此,我们从图12所示的两个维度来讨论政策影响。在第一个维度中,风险的空间覆盖范围分为全球区域和目标区域,如公式(1)所示。全球区域指的是针对整个城市或更大行政区域的管理和控制(①),而目标区域指的是根据风险等级划分的特定区域(②)。在第二个维度中,受公式(7)的限制,乘客便利性和节能各有侧重,因此有三种类型的目标,即以乘客便利性为导向的目标(PC)、以节能为导向的目标(EE)和两者兼顾的目标(PC & EE)。因此,有六种组合响应式客流控制政策①-PC、①-EE、①-PC & EE、②-PC、②-EE、②-PC & EE(分别简称为政策 A、B、C、D、E 和 F)。如下文所述,控制政策的适用取决于突发公共卫生事件的轻重缓急和阶段。
在突发公共卫生事件爆发初期(如2020年COVID-19在武汉的首次爆发),政策 A仅提供低运力,避免给乘客带来不便。在这一阶段,突发公共卫生事件的扩散机制尚不明确,客运需求大幅萎缩,主要用于基本出行,可通过低运力供给(Lu 等,2022) 。随着出行需求的缓慢恢复和突发事件控制能力的提高,运营商可能仍会采取保守的立场,执行政策B,以节省相对较低的出行需求的运营成本。在细化层面上,当出行需求得到一定程度的恢复时,运营方应执行政策C,以平衡根据第4节中案例1的结果,决策支持模型可以在不同的列车容量利用率和不便程度下,输出带有客流控制的城市轨道交通网络的开行设计。
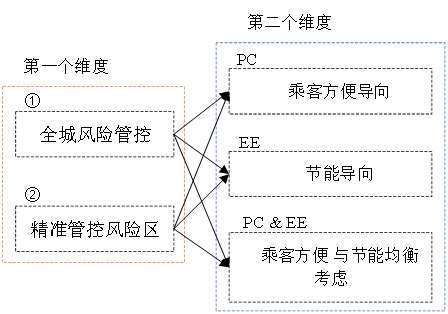
图12. 突发公共卫生事件的管控策略
由于大规模疫苗接种和季节性效应,突发公共卫生事件的负面影响(如确诊病例数)可能会大幅减少。当突发事件仅在局部地区反复爆发时,全球范围的风险控制是不可持续的,也是不必要的。就COVID-19而言,虽然 ,但对于可能出现的新变种(Saha等,2021年),在全球范围内消除感染风险的可能性不大,但传播机制已被充分了解,这为采取针对性措施提供了机会,对乘客便利性和运营成本的负面影响较小。与A-C政策相对应,D-F政策的重点是针对不同目标的风险区域进行有针对性的管理和控制。其中,政策F兼顾了乘客便利性和节能,最适合后疫情时代。正如第4节中案例2的数值结果所证实的那样,有针对性的客流控制在各项指标上都优于广泛控制。总之,在不同的突发公共卫生事件场景和不同的控制目标下,决策支持模型及其潜在的扩展功能有助于有效地运营城市轨道交通系统。
5.2.结论和未来工作
突发公共卫生事件给公共交通的管理和控制政策带来了挑战。为防止突发公共卫生事件的负面影响在城市轨道交通系统中扩散,本文建立了一个以节能为导向的决策支持模型,在列车容量利用率的约束下确定列车发车频次和 客流控制。该决策支持模型采用MILP方法,可有效求解。考虑到2021年底中国西安市COVID-19的爆发,案例研究证明,考虑到路径流量控制给乘客带来的不便,决策支持模型可以有效降低能耗。结果表明,对风险区域进行有针对性的管理可以在减少乘客不便的同时实现节能。
基于所提出的模型框架,今后还可以开展一些研究。首先,还可以探讨其他运营措施,如在风险区域跳站和部分关闭车站,以防止大流行病的传播。其次,应区分突发公共卫生事件下乘客偏好的异质性。例如,一些乘客可能会拒绝规划途经任何风险区域的路线。第三,对于需要多模式换乘的乘客,应整合城市轨道交通与其他交通方式之间的协调。最后,网络拓扑结构也是影响疫情传播和能源消耗的一个重要因素,也应加以探讨。

扫描二维码阅读原文
参考文献
[1]Borjigin, S. G., He, Q., & Niemeier, D. A. (2023). COVID-19 transmission in US transit buses: A scenario-based approach with agent-based simulation modeling (ABSM). Communications in Transportation Research, 3, 100090.
[2]Canca, D., & Zarzo, A. (2017). Design of energy-Efficient timetables in two-way railway rapid transit lines. Transportation Research Part B: Methodological, 102, 142–161.
[3]de Palma, A., Vosough, S., & Liao, F. (2022). An overview of effects of COVID-19 on mobility and lifestyle: 18 months since the outbreak. Transportation Research Part A: Policy and Practice, 159, 372–397.
[4]Elias, W., & Zatmeh-Kanj, S. (2021). Extent to which COVID-19 will affect future use of the train in Israel. Transport Policy, 110, 215–224.
[5]Gao, Z., & Yang, L. (2019). Energy-saving operation approaches for urban rail transit systems. Frontiers of Engineering Management, 6(2), 139–151.
[6]Gkiotsalitis, K., & Cats, O. (2022). Optimal frequency setting of metro services in the age of COVID-19 distancing measures. Transportmetrica A: Transport Science, 18(3), 807–827.
[7]Guo, X., Wang, D. Z. W., Wu, J., Sun, H., & Zhou, L. (2020). Mining commuting behavior of urban rail transit network by using association rules. Physica A: Statistical Mechanics and Its Applications, 559, 125094.
[8]Harris, J. E. (2020). The Subways Seeded the Massive Coronavirus Epidemic in New York City. In SSRN Electronic Journal. National Bureau of Economic Research.
[9]Huang, K., & Liao, F. (2023). A novel two-stage approach for energy-efficient timetabling for an urban rail transit network. Transportation Research. Part E: Logistics and Transportation Review.
[10]Huang, K., Liao, F., & Gao, Z. (2021). An integrated model of energy-efficient timetabling of the urban rail transit system with multiple interconnected lines. Transportation Research Part C: Emerging Technologies, 129, 103171.
[11]Huang, K., Liao, F., Lyu, H., & Gao, Z. (2023). Assessment of the tradeoff between energy efficiency and transfer opportunities in an urban rail transit network. Sustainable Energy Technologies and Assessments, 58, 103360.
[12]Huang, Y., Yang, L., Tang, T., Gao, Z., & Cao, F. (2017). Joint train scheduling optimization with service quality and energy efficiency in urban rail transit networks. Energy, 138, 1124–1147.
[13]Jia, J., Chen, Y., Wang, Y., Li, T., & Li, Y. (2021). A new global method for identifying urban rail transit key station during COVID-19: A case study of Beijing, China. Physica A: Statistical Mechanics and Its Applications, 565, 125578.
[14]Kang, L., Sun, H., Wu, J., & Gao, Z. (2020). Last train station-skipping, transfer-accessible and energy-efficient scheduling in subway networks. Energy, 206, 118127.
[15]Lu, Y., Yang, L., Yang, K., Gao, Z., Zhou, H., Meng, F., & Qi, J. (2022). A distributionally robust optimization method for passenger flow control strategy and train scheduling on an urban rail transit line. Engineering, 12, 202–220.
[16]Luo, Q., Forscher, T., Shaheen, S., Deakin, E., & Walker, J. L. (2023). Impact of the COVID-19 pandemic and generational heterogeneity on ecommerce shopping styles–A case study of Sacramento, California. Communications in Transportation Research, 3, 100091.
[17]Lv, H., Zhang, Y., Huang, K., Yu, X., & Wu, J. (2019). An energy-efficient timetable optimization approach in a bi-directionurban rail transit line: A mixed-integer linear programming model. Energies, 12(14), 1–24.
[18]Mo, P., Yang, L., D’Ariano, A., Yin, J., Yao, Y., & Gao, Z. (2019). Energy-efficient train scheduling and rolling stock circulation planning in a metro line: a linear programming approach. IEEE Transactions on Intelligent Transportation Systems, 21(9), 3621–3633.
[19]Ning, J., Zhou, Y., Long, F., & Tao, X. (2018). A synergistic energy-efficient planning approach for urban rail transit operations. Energy, 151, 854–863.
[20]Pan, D., Zhao, L., Luo, Q., Zhang, C., & Chen, Z. (2018). Study on the performance improvement of urban rail transit system. Energy, 161, 1154–1171.
[21]Saha, S., Tanmoy, A. M., Tanni, A. A., Goswami, S., Sium, S. M. Al, Saha, S., Islam, S., Hooda, Y., Malaker, A. R., Anik, A. M., Haq, M. S., Jabin, T., Hossain, M. M., Tabassum, N., Rahman, H., Hossain, M. J., Islam, M. S., & Saha, S. K. (2021). New waves, new variants, old inequity: a continuing COVID-19 crisis. BMJ Global Health, 6(8), e007031.
[22]Sun, X., Wandelt, S., & Zhang, A. (2023). Why are COVID-19 travel bubbles a tightrope walk? An investigation based on the Trans-Tasmanian case. Communications in Transportation Research, 3, 100089.
[23]Tirachini, A., & Cats, O. (2020). COVID-19 and Public Transportation: Current Assessment, Prospects, and Research Needs. Journal of Public Transportation, 22(1).
[24]Wang, L., Yang, L., Gao, Z., & Huang, Y. (2017). Robust train speed trajectory optimization: A stochastic constrained shortest path approach. Frontiers of Engineering Management, 4(4), 408.
[25]Wang, Q., Guo, J., Ge, Y., Liang, C., Xian, K., Diao, J., & Ma, Y. (2021). Practice and thoughts on reservation travel in Beijing Metro Stations. Urban Transport of China, 19(01), 89–94.
[26]Xie, J., Zhang, J., Sun, K., Ni, S., & Chen, D. (2021). Passenger and energy-saving oriented train timetable and stop plan synchronization optimization model. Transportation Research Part D: Transport and Environment, 98, 102975.
[27]Yang, S., Chen, Y., Dong, Z., & Wu, J. (2023). A collaborative operation mode of energy storage system and train operation system in power supply network. Energy, 276, 127617.
[28]Yin, J., Cao, X. J., & Huang, X. (2021). Association between subway and life satisfaction: Evidence from Xi’an, China. Transportation Research Part D: Transport and Environment, 96, 102869.
[29]Zeng, G., Sun, Z., Liu, S., Chen, X., Li, D., Wu, J., & Gao, Z. (2021). Percolation-based health management of complex traffic systems. Frontiers of Engineering Management, 8(4), 557–571.
[30]Zhang, L., He, D., He, Y., Liu, B., Chen, Y., & Shan, S. (2022). Real-time energy saving optimization method for urban rail transit train timetable under delay condition. Energy, 258, 124853.
[31]Zhang, P., Yang, X., Wu, J., Sun, H., Wei, Y., & Gao, Z. (2022). Coupling analysis of passenger and train flows for a large-scale urban rail transit system. Frontiers of Engineering Management, 1–12.
[32]Zhou, J., & Koutsopoulos, H. N. (2021). Virus transmission risk in urban rail systems: Microscopic simulation-based analysis of spatio-temporal characteristics. Transportation Research Record, 2675(10), 120–132.
[33]Zhou, W., Huang, Y., Deng, L., & Qin, J. (2023). Collaborative optimization of energy-efficient train schedule and train circulation plan for urban rail. Energy, 263, 125599.
推荐阅读
1.FEM Dec 2024, Volume 11 Issue 4下一代智慧交通系统—构想一个碳中和、互联、智能、公平的交通专题摘要
2.FEM Sep 2024, Volume 11 Issue 3 内容摘要
3.FEM Jun 2024, Volume 11 Issue 2 内容摘要
4.FEM Mar 2024, Volume 11 Issue1内容摘要
5.FEM Dec 2023, Volume 10 Issue 4 内容摘要
6.FEM Sep 2023, Volume 10 Issue 3 内容摘要
7.FEM Jun 2023, Volume 10 Issue 2内容摘要
8.FEM 2023, Volume 10 Issue 1 后疫情时代供应链韧性的提升专题内容摘要
9.城市自动驾驶交通全局调度模式的框架、模型和算法
10.重大基础设施项目可供性:一种改善利益相关者管理和项目可持续的新视角
11.专刊: 下一代智慧交通系统—构想一个碳中和、互联、智能、公平的交通
12.TK1井万米深地工程技术进展
13.项目学习:大型基础设施开发的启示
14.白鹤滩水电站工程建设关键技术创新
15.人民网报道:重要度驱动的维护策略 助力智慧城市基础设施韧性建设
16.项目学习:大型基础设施开发的启示
17.共享单车系统的需求可预测性:一项站点级别的分析
18.中国公路交通的直接能源回弹效应
19.城市轨道交通中断管理: 研究进展及未来方向
《前沿》系列英文学术期刊
由教育部主管、高等教育出版社主办的《前沿》(Frontiers)系列英文学术期刊,于2006年正式创刊,以网络版和印刷版向全球发行。系列期刊包括基础科学、生命科学、工程技术和人文社会科学四个主题,是我国覆盖学科最广泛的英文学术期刊群,其中13种被SCI收录,其他也被A&HCI、Ei、MEDLINE或相应学科国际权威检索系统收录,具有一定的国际学术影响力。系列期刊采用在线优先出版方式,保证文章以最快速度发表。
中国学术前沿期刊网
http://journal.hep.com.cn

特别声明:本文转载仅仅是出于传播信息的需要,并不意味着代表本网站观点或证实其内容的真实性;如其他媒体、网站或个人从本网站转载使用,须保留本网站注明的“来源”,并自负版权等法律责任;作者如果不希望被转载或者联系转载稿费等事宜,请与我们接洽。