论文标题：Approximation of Caputo Fractional Derivative and Numerical Solutions of Fractional Differential Equations

论文链接：https://doi.org/10.3390/fractalfract7100750

期刊名：Fractal and Fractional

期刊主页：https://www.mdpi.com/journal/fractalfract

研究背景与价值

分数阶微分方程是不同领域科学中对复杂过程进行建模的重要手段。来自保加利亚索非亚林业大学的 Yuri Dimitrov，和他的研究团队一起构建了以多项对数函数为生成函数的 Caputo 分数阶导数近似及其渐近展开公式，证明了近似的收敛性，并推导得到其误差范围与阶数。将此近似方法用于构建两类典型分数阶方程，二项常分数阶微分方程和时间分数阶 Black-Scholes 方程。近似的性质被用于证明有限差分方案的收敛性和阶数，并获得数值方法的误差范围。数值实验结果和理论结果基本相符。

研究过程

借助多项对数函数，推导 Caputo 导数近似公式

本文首先明确了多项对数函数的定义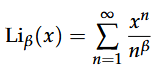并给出其关键展开式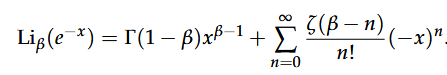在前人的研究基础上，通过应用上述多项对数函数展开式，推导得到Caputo 导数近似公式

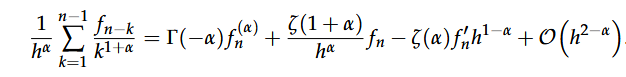
计算近似公式的误差估计

为分析近似公式的误差，作者引入辅助函数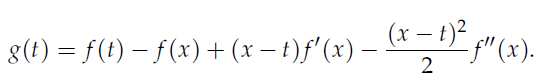和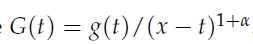，结合梯形法则误差分析，推导出不同近似公式的误差

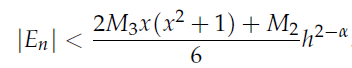
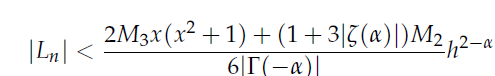
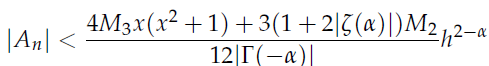
实际应用

1. 应用于二项常分数阶微分方程的数值计算

二项常分数阶微分方程形式为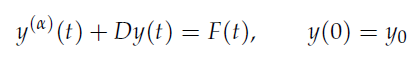

将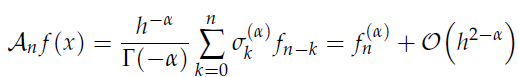应用于该方程，对时间离散后构建有限差分格式，得到数值解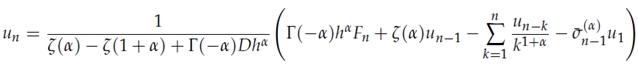递推公式，同时确定初始条件u_1的取值。通过相关的定理完成收敛性分析，得出误差的范围。数值实验选取具体方程实例，计算不同步长h、参数α下的误差阶数，当α=0.75，h=0.025时，误差阶数约为1.25，符合2-α=1.25的理论预期，验证了方法有效性。

2. 应用于时间分数阶 Black-Scholes 方程的数值计算

时间分数阶 Black-Scholes 方程用于期权定价建模，形式为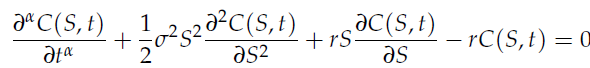

通过变量替换将方程转化为便于计算的形式，将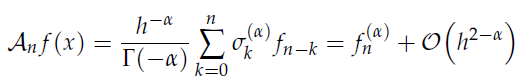应用于该方程，构建隐式有限差分格式，得到数值解满足的线性方程组及初始边界条件。得出误差向量的范围，验证收敛性。数值实验分析了参数α下的期权价格，体现了方法在金融场景的实用性。

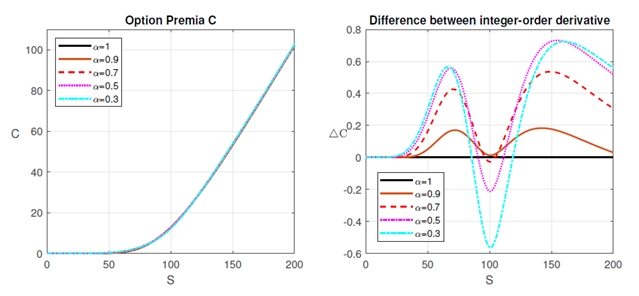
各种参数a的期权溢价（左图）以及它们与整阶模型的期权溢价（右图）之间的差异

Fractal and Fractional 期刊介绍

主编：Carlo Cattani, University of Tuscia, Italy

期刊主题涵盖包括分形和分数阶微积分基础研究及其在不同科学和工程领域中的应用研究。现已被 SCIE (Web of Science)、Scopus 等重要数据库收录，JCR category rank: 22/136 (Q1)，中国科学院2区。