近期，中国科学院大学工程科学学院长聘教轨副教授刘扬在《自然—机器智能》（Nature Machine Intelligence）上，发表了题为Encoding physics to learn reaction-diffusion process的研究成果。该研究提出了新的物理知识嵌入深度学习架构即PeRCNN，用于偏微分方程（PDE）正反问题求解、非线性时空动力系统建模和控制方程发现，旨在改善复杂时空动力系统基于稀疏和噪声数据建模的准确性和可解释性。该工作建立了强制编码物理结构的循环卷积神经网络框架，有效解决了网络对训练数据的依赖性，突破了神经网络模型不可解释的瓶颈，同时，提升了模型的外推和泛化性，在各类反应扩散系统（RD）问题场景实现验证。

一般而言，由于先验知识有限，且系统变量的非线性过程难以用明确的偏微分方程（PDE）公式描述，复杂时空动力系统建模和仿真是颇具挑战性的任务。常见的机器学习方法需要依赖大量训练数据，存在可解释性差、泛化性弱、误差不可控等基础科学问题。将先验物理知识（如控制方程）作为约束加入深度学习，在一定程度上增强模型的可解释性、缓解数据依赖性。然而，现有的基于物理信息的深度学习方法通常需要通过软约束来施加物理定律，且模型表现很大程度上取决于超参数的恰当设置。因此，亟需发展新的知识嵌入学习模型，以在数据中捕捉潜在的时空动态演化机制。

科研人员提出了新的学习模型即物理编码递归卷积神经网络（PeRCNN），如图1所示。PeRCNN的主要优点是可以将先验物理知识结构编码到网络中，采用时空学习范式，旨在建立通用且鲁棒学习模型，能够保证所得到的网络严格服从给定的先验物理知识（如PDE结构、初始和边界条件），使得网络具有可解释性。模型通过循环卷积神经网络对给定的物理结构进行编码，提高在稀疏和噪声数据情况下学习复杂时空动力学的能力。

图1. PeRCNN模型图

通过大量数值实验，该工作展示了PeRCNN对反应扩散型偏微分方程的正向（图2）和反向（图3）问题分析的有效性。与几个基线模型的比较表明，物理编码学习范式具有独特的外推能力、对数据噪声或稀疏数据的泛化能力和鲁棒性。在数据驱动仿真实验中，PeRCNN取得了SOTA结果；PeRCNN的平坦误差传播曲线（图4）证明了PeRCNN显著的外推和泛化能力，意味着该方法不仅能够准确地预测复杂时空动力系统的演变，而且能够捕捉模型背后的物理机制，在应对新的工况时能够展现出一定的通用性。

图2. 实验结果（PDE正问题）

图3. 实验结果（PDE反问题）

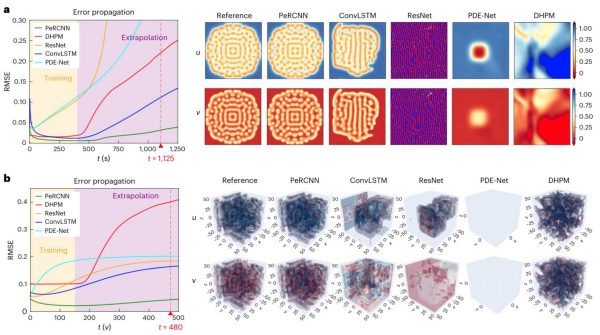
图4. 实验结果（数据驱动建模，误差传播和外推图示）

此外，该工作将PeRCNN与稀疏回归算法相结合，解决了潜在PDE发现问题（图5），可进一步在学习模型中提取控制底层物理机制的解析表达式。耦合方案使得模型能够迭代优化网络参数，并对发现的PDE结构和系数进行微调，获得最终PDE的简约表达形式，在稀疏带噪声的测量数据中准确可靠地发现潜在的物理定律。

图5. 控制偏微分方程发现流程图

本研究证明了PeRCNN在各种反应扩散系统上的有效性，但该模型在理论上适用于其他类型的时空动力系统，如补充材料展示了带对流项的二维Burgers方程、雷诺数为1000的Kolmogorov湍流（NS方程）。

上述成果为复杂时空动力系统数据驱动建模领域带来了新进展，为科学家和工程师提供了更强大的工具来探讨和预测自然和工程现象。这种结合深度学习和先验物理的方法，有望在流体力学、生物化学、环境科学、工程学和材料科学等学科领域应用中发挥重要作用。（来源：中国科学院大学）

相关论文信息：https://doi.org/10.1038/s42256-023-00685-7