论文标题:Super solutions of the model RB(随机RB模型的超解研究)
期刊:Frontiers of Computer Science
作者:Guangyan ZHOU, Wei XU
发表时间:15 Dec 2022
DOI:10.1007/s11704-021-1189-8
微信链接:点击此处阅读微信文章
原文信息
标 题:
Super solutions of the model RB
原文链接:
https://journal.hep.com.cn/fcs/EN/10.1007/s11704-021-1189-8
引用格式:
Guangyan ZHOU, Wei XU. Super solutions of the model RB. Front. Comput. Sci., 2022, 16(6): 166406
公众号推文链接:
随机RB模型的超解研究
01
导读
约束满足问题(CSP)在计算机科学、统计物理和信息理论领域发挥着重要作用。CSP实例涉及一组变量和一组约束,任务是找到解决方案(满足所有约束的变量分配)或证明不可解性。RB模型是一种CSP模型,旨在克服标准模型B的微小不可满足性。已经建立了可满足性相变和精确阈值点,从模型RB生成的基准已广泛用于算法竞赛。从统计物理学角度进行的研究也很有成果,其中揭示了解空间的更多结构,如聚类阶段。
RB模型的一个实例I包含一组有限的变量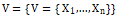 和约束
和约束 。每个的域
。每个的域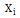 是
是 ,其中
,其中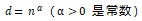 。每个约束
。每个约束 都包含随机选择
都包含随机选择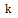 的不同变量
的不同变量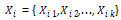 ,以及一组满足
,以及一组满足 的值元组
的值元组 。如果分配给的值的元组
。如果分配给的值的元组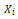 处于对应关系
处于对应关系 中,则满足约束
中,则满足约束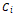 。
。
超级解是在许多组合优化和决策问题中,为了形式化具有一定鲁棒性或稳定性的解而引入的概念。为了量化鲁棒性,将(a,b)-超级解引入约束规划。具体来说,(a,b)-超级解决方案是这样一种解决方案,即如果分配给变量的值不再可用,则可以通过为这些变量分配新值a和最多其他变量b来修复解决方案.(1,0)-超级解已经研究了固定的 和用于随机(3+p)-SAT的模型RB。在本文中,文章选择了不受和限制的模型RB的(1,1)-超解,并通过渐近一阶矩论证证明了以下结果。
和用于随机(3+p)-SAT的模型RB。在本文中,文章选择了不受和限制的模型RB的(1,1)-超解,并通过渐近一阶矩论证证明了以下结果。
定理1 使Y为模型RB的(1,1)-超级解的个数。然后

02
定理1的证明
文章将使用与上文相同的符号直到等式 .使:
.使:

从而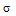 满足C;使
满足C;使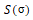 成为
成为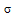 是I的解决方案的事件,
是I的解决方案的事件, 是存在对于
是存在对于 的另一个解
的另一个解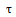 ,使得
,使得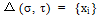 或
或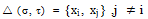 ;
; 是
是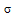 是
是 的(1,1)-超解。设
的(1,1)-超解。设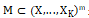 是m个无序约束
是m个无序约束 的所有可能的多集合,c是被选为随机实例的约束集合
的所有可能的多集合,c是被选为随机实例的约束集合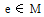 的结果。然后是
的结果。然后是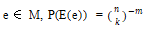 和
和 。可以得到
。可以得到
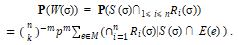 (1)
(1)
通过包含或排除,文章给出了以下边界(足够严谨),故可以进行估计
 (2)
(2)
在下文中,假设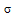 是I包含变量的一组约束的解,同时
是I包含变量的一组约束的解,同时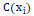 是包含变量的约束集
是包含变量的约束集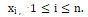 .使
.使 。
。
Lemma 1 注意到有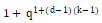 对于τ来说有可能的方法可以在C中分配变量,因此
对于τ来说有可能的方法可以在C中分配变量,因此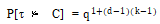 ,因此Lemma1如下:
,因此Lemma1如下:
使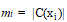 ,从Lemma 1 可以得出
,从Lemma 1 可以得出
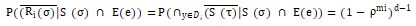 (3)
(3)
Lemma 2 认为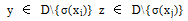 ,如果
,如果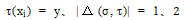 分配
分配 和
和 那么对于任何
那么对于任何 则有:
则有:

证明 假设有一个正好是一个常见的赋值,
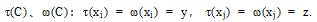
因此:
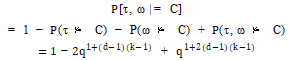
代入 , 到 Lemma 2,可以推导出
, 到 Lemma 2,可以推导出
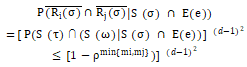 (4)
(4)
梳理公式(2), (3) 和 (4) 可以得到
 (5)
(5)
●亚临界区域: . 通过等式 .
. 通过等式 .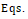 (1)和 (5),得到
(1)和 (5),得到
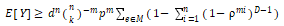
假设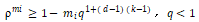 , 则
, 则
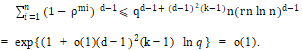
因此如果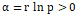 , 那么
, 那么 将倾向于
将倾向于
●亚临界区域:
假设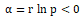 ,通过等式.
,通过等式.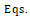 (1)和(5),得到
(1)和(5),得到
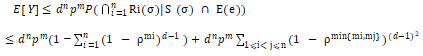
请注意: ,同时
,同时
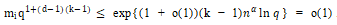 .
.
然后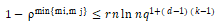 ,因此:
,因此:

因此 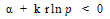 , 随后
, 随后

03
结论
文章证明了模型RB的期望数量的(1,1)-超解经历了从0到无穷大的相变。有趣的是,阈值与标准可满足性阈值完全相同。此外,定理1中r的约束与约束大小k无关。超级解可以被视为标准解的某种类型的“局部最大”子集,因此文章认为其结果从另一个方面反映了解空间的结构和解的稳定性。对于未来的工作,不论 是一个几乎可以肯定(1,1)-满足或不满足的临界点仍然是未知的。
是一个几乎可以肯定(1,1)-满足或不满足的临界点仍然是未知的。
解读:戴西件 南昌大学第二附属医院
审核:张 琨 合肥工业大学

Frontiers of Computer Science
Frontiers of Computer Science (FCS)是由教育部主管、高等教育出版社和北京航空航天大学共同主办、SpringerNature 公司海外发行的英文学术期刊。本刊于 2007 年创刊,双月刊,全球发行。主要刊登计算机科学领域具有创新性的综述论文、研究论文等。本刊主编为周志华教授,共同主编为熊璋教授。编委会及青年 AE 团队由国内外知名学者及优秀青年学者组成。本刊被 SCI、Ei、DBLP、INSPEC、SCOPUS 和中国科学引文数据库(CSCD)核心库等收录,为 CCF 推荐期刊;两次入选“中国科技期刊国际影响力提升计划”;入选“第4届中国国际化精品科技期刊”;入选“中国科技期刊卓越行动计划项目”。
《前沿》系列英文学术期刊
由教育部主管、高等教育出版社主办的《前沿》(Frontiers)系列英文学术期刊,于2006年正式创刊,以网络版和印刷版向全球发行。系列期刊包括基础科学、生命科学、工程技术和人文社会科学四个主题,是我国覆盖学科最广泛的英文学术期刊群,其中12种被SCI收录,其他也被A&HCI、Ei、MEDLINE或相应学科国际权威检索系统收录,具有一定的国际学术影响力。系列期刊采用在线优先出版方式,保证文章以最快速度发表。
中国学术前沿期刊网
http://journal.hep.com.cn

特别声明:本文转载仅仅是出于传播信息的需要,并不意味着代表本网站观点或证实其内容的真实性;如其他媒体、网站或个人从本网站转载使用,须保留本网站注明的“来源”,并自负版权等法律责任;作者如果不希望被转载或者联系转载稿费等事宜,请与我们接洽。