近日，德国柏林自由大学Jacopo Rizzo团队研究了有限计算资源下的纠缠理论。2025年10月22日出版的《自然—物理学》杂志发表了这项成果。

量子信息理论的核心是精确量化操纵量子资源的极限。然而，标准的信息论分析并没有考虑执行某些任务所涉及的实际计算复杂性。

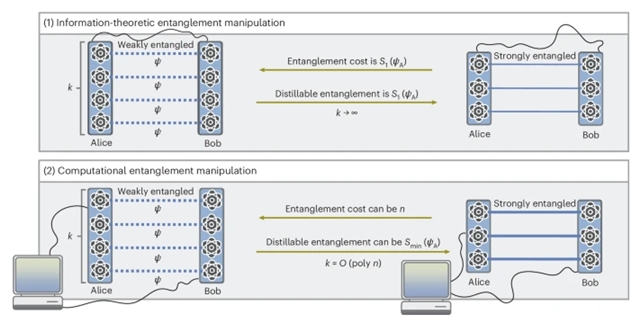
研究组在纠缠理论领域内解决了这个问题，发现计算效率的考虑实质上改变了纠缠资源可以实现的目标。他们考虑了两个关键的优点：计算可蒸馏纠缠和计算纠缠成本。这些措施量化了纠缠比特的最佳速率，这些纠缠比特可以从n量子位二元纯态的许多相同副本中提取或稀释，使用计算效率的局部操作和经典通信。

研究组证明了计算纠缠度量与它们的信息论对应度量有很大的不同。而信息论的可蒸馏纠缠是由约化态的冯·诺依曼熵决定的，研究组表明最小熵控制计算效率设置。另一方面，计算效率高的纠缠稀释要求最大限度地消耗纠缠比特，即使是在几乎没有纠缠的状态下。此外，在最坏的情况下，即使存在对状态的有效描述并且完全已知，也不会比状态不可知协议获得任何优势。该发现为测量和测试冯·诺伊曼熵建立了样本复杂度界限，这是有效状态压缩和有效局部断层扫描协议的基本限制。

附：英文原文

Title: Entanglement theory with limited computational resources

Author: Leone, Lorenzo, Rizzo, Jacopo, Eisert, Jens, Jerbi, Sofiene

Issue&Volume: 2025-10-22

Abstract: The precise quantification of the limits to manipulating quantum resources lies at the core of quantum information theory. However, standard information-theoretic analyses do not consider the actual computational complexity involved in performing certain tasks. Here we address this issue within the realm of entanglement theory, finding that accounting for computational efficiency substantially changes what can be achieved using entangled resources. We consider two key figures of merit: the computational distillable entanglement and the computational entanglement cost. These measures quantify the optimal rates of entangled bits that can be extracted from or used to dilute many identical copies of n-qubit bipartite pure states, using computationally efficient local operations and classical communication. We demonstrate that computational entanglement measures diverge considerably from their information-theoretic counterparts. Whereas the information-theoretic distillable entanglement is determined by the von Neumann entropy of the reduced state, we show that the min-entropy governs the computationally efficient setting. On the other hand, computationally efficient entanglement dilution requires maximal consumption of entangled bits, even for nearly unentangled states. Furthermore, in the worst-case scenario, even when an efficient description of the state exists and is fully known, one gains no advantage over state-agnostic protocols. Our findings establish sample-complexity bounds for measuring and testing the von Neumann entropy, fundamental limitations on efficient state compression and efficient local tomography protocols.

DOI: 10.1038/s41567-025-03048-8

Source: https://www.nature.com/articles/s41567-025-03048-8